四分割法の問題は、一見とっつきにくい問題に見えますが、力の構造計算に比べて非常に簡単です。出題形式がワンパターンなので、一度過去問を解いて理解しておけば得点源にできる範囲ではないかと思いますので、この機会に学習してしまいましょう!この機会に周辺の内容も掘り下げつつ勧めたいと思います。

出題もワンパターンで、個人的には得点しやすい内容だと思います。
過去の出題例より
早速ですが、過去の出題を参考に説明していきたいと思います。下の図の壁率比を求める問題です。
(条件は木造軸組工法の2階建て、1,2階の平面形状は同じで平家部分はないものとします。また、耐力壁の壁倍率は2とする)
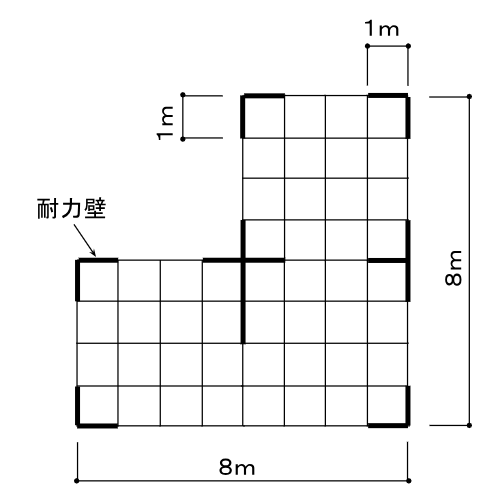
まずは語句の説明からします。
壁率比とは
計算式にすると…
壁率比 = 壁量充足率の小さい方 / 壁量充足率の大きい方
となっております。
また、壁率比は0.5以上であることを確認する必要があります。(ただし、側端部の壁量充足率がいずれも1を超える場合、偏心率が0.3以下の場合は除きます)壁率比は梁間方向及びけた行方向のそれぞれ計算します。
壁量充足率とは
壁率比を求めるのに必要な壁量充足率とは、以下の計算式で求められます。
壁量充足率 = 存在壁量 / 必要壁量
- 存在壁量:壁倍率 x 側端部の軸組の長さ の和
- 必要壁料:階の床面積に乗ずる数値 x 側端部の床面積
と、なっております。また、壁量充足率は各側端部で計算します。
壁倍率と階の床面積に乗ずる数値は問題文に記載されているケースが多いです。
ではこれらを踏まえて実際に問題を解いていきましょう!
存在壁量を求める
先述した計算式より、壁率比を求めるには壁量充足率が必要で、壁量充足率を求めるには存在壁量と必要壁量が必要になります。
存在壁量は各側端部事に、「壁倍率」x「側端部の軸組の長さ」の和 で求めます。
「壁倍率」は題意より、2と決まっております。
「側端部の軸組の長さ」は、図中の耐力壁の長さのことになります。
図を見て確認していきましょう。
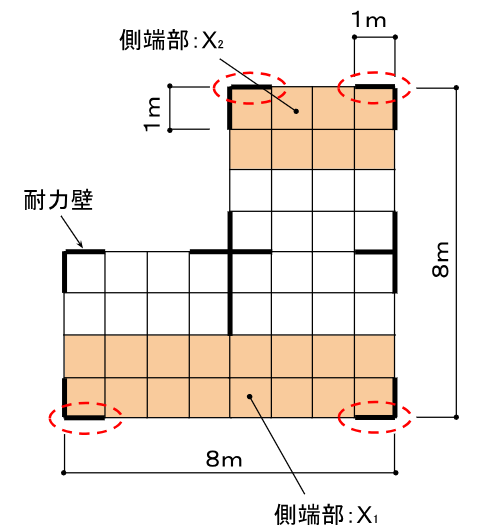
まずは、側端部X₁とX₂から。図ではそれぞれの側端部を色付けし、X方向に影響する耐力壁に赤マルで囲いました。
X₁の存在壁量は
「壁倍率 2」x「側端部の軸組の長さ 1m」+「壁倍率 2」x「側端部の軸組の長さ 1m」
= 4
X₂の存在壁量は
「壁倍率 2」x「側端部の軸組の長さ 1m」+「壁倍率 2」x「側端部の軸組の長さ 1m」
= 4
となります。次にY方向を確認していきます。
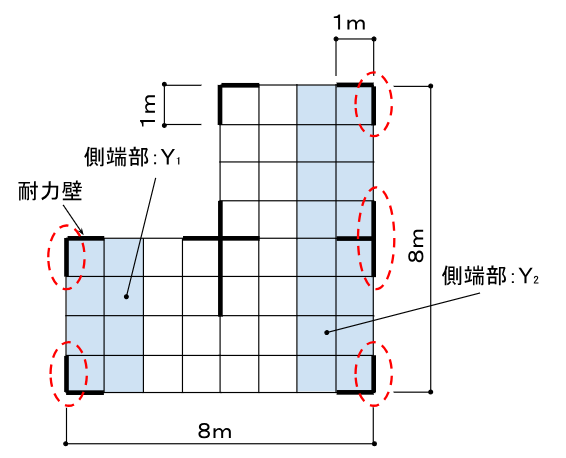
Y₁の存在壁量は
「壁倍率 2」x「側端部の軸組の長さ 1m」+「壁倍率 2」x「側端部の軸組の長さ 1m」
= 4
Y₂の存在壁量は
「壁倍率 2」x「側端部の軸組の長さ 1m」+「壁倍率 2」x「側端部の軸組の長さ 2m」+「壁倍率 2」x「側端部の軸組の長さ 1m」
= 8
必要壁量を求める
次に必要壁量を求めます。
必要壁量は、「階の床面積に乗ずる数値」 x「 側端部の床面積」で計算します。
「階の床面積に乗ずる数値」については、この問題では示されていませんが建築基準法施工令より33cm/m²となります。壁率比を求める際に相殺されてしますので考えなくてよいからと思われます。過去問においては題意で示されているケースもあります。
「側端部の床面積」については、先程、存在壁量で使用した図の色付きの面積部分になります。
以上のことから
X₁の必要壁量は16m²、X₂の必要壁量は8m²、Y₁の必要壁量は8m²、Y₂の必要壁量は16m²となります。
壁量充足率を求める
壁量充足率 = 存在壁量 / 必要壁量 より求められます。
先程の数値を元に計算しますと、
X₁=(2x1m)x2 /(8mx2m) = 4 / 16 =0.25
同様に計算していき
X₂=0.5、Y₂=0.5、Y₂=0.5 となります。
壁率比を求める
X方向の壁率比
= 壁量充足率の小さい方 X₁ / 壁量充足率の大き方 X₂
= 0.25 / 0.5 = 0.5
Y方向の壁倍率
= 壁量充足率の小さい方 Y₁ / 壁量充足率の大き方 Y₂
= 0.5 / 0.5 = 1.0
X、Yとも0.5以上である。
以上がこの問題の解答手順となります。
補足 壁倍率について
過去の出題より、四分割法とは別に軸組の壁倍率に関する問題がありましたので、ポイントをまとめておきました。
- 構造用面材と筋かいを併用した場合の軸組の壁倍率はそれぞれの数値の和とできる。
→◯ - 同じボードを2枚重ねて片面にのみ釘で打ち付けた場合、そのボードを単体で使用したときの数値の2倍の壁倍率とできる。
→✕ 単純に2倍できない。ただし、両面に1枚づつ釘打ちした場合は2倍となる。 - 軸組の壁倍率が5を超える場合は、5となる。
→◯
今回は以上になります。少しでもお役に立てば嬉しいです。




コメント