学科Ⅳの構造でNo.7の問題は構造力学として出題があり、計算問題として出題される場合と、文章問題で出題される場合があります。特に振動からはモデルを用いた固有周期にかかる問題が印象に残りがちですが、文章問題として出題される場合には、キーワードを知っていないと解けない問題がありますので一度整理しておくのが良いと思います。近年の出題(令和6年、令和3年)をもとにまとめてみました。

固有周期からの出題って、基本式を覚えて対応するんじゃないの?あのバネのモデルの。

文章形式の出題の場合、それだけでは対応できないこともありますね。

せっかく基本式覚えたのに…

平成20年以前に出ていた問題が最近になってまたよく見られるようになりました。

問題に出されるキーワード自体は難しくありませんから、ちょっとおさらいしておきましょう。
固有周期(振動)
固有周期
これは今回の重要なキーワードというわけではありませんが、やはりメインの基本式なのでおさらいしておきます。
ちなみに文章問題を解く際は、こちらの基本式に当てはめて正誤を判断することがありますので覚えておく必要はあります。
その基本式がこちら↓
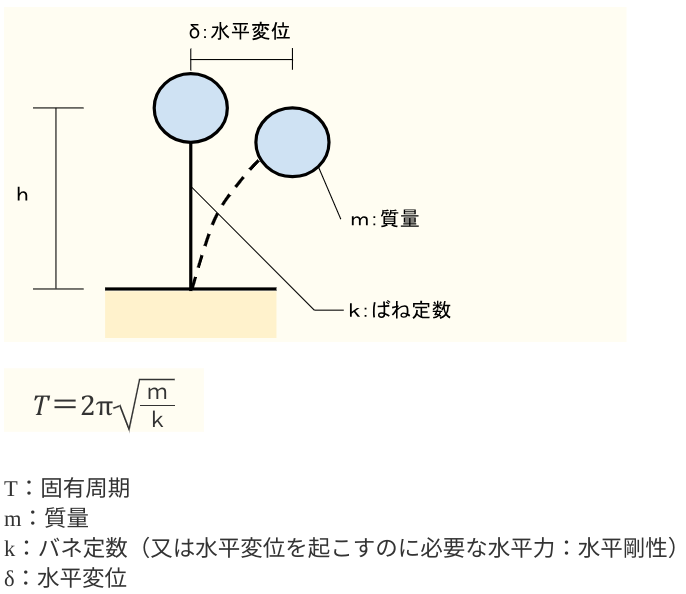
ちなみにこれを覚えることで解答できるようになる過去問題は次のこんな感じです↓
過去問題より
(R03-07より)
2.建築物の固有周期は、質量が同じ場合、水平剛性が大きいものほど短くなる。
こちらはの枝は正しいでしょうか、それとも誤り?
振動モード
ココからが今回の本題ですね。
「振動モード」
聞いたことありますでしょうか。聞き慣れないと思いますがこれまでに数回出題されています。直近では令和6年、令和3年です。
「振動モード」とは、振動している構造物の同時刻における振幅の分布を示すもの。
うーん、難しいですね。
ただ出題されるのは以下の内容になります。
多質点系の振動モード
モデルとしてココでは3質点系モデルを使用します。
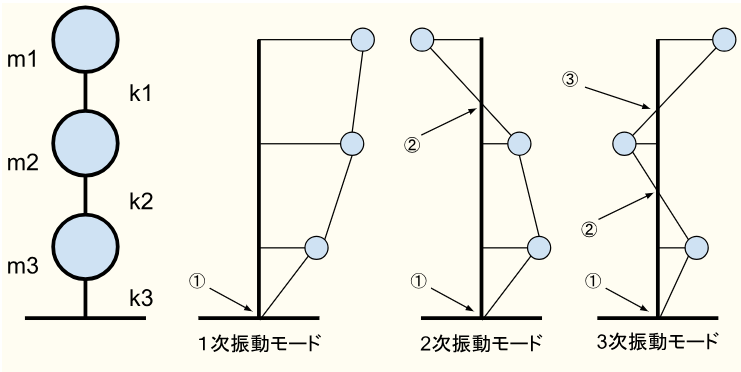
※上図の①〜③は節(不動点)を示しています。
図のモデルを用いて振動モードを説明すると…
3質点系モデルの場合は、3個の節があり、3個の固有周期があり、3次振動モードによる3次固有周期まである。ということになります。
つまり…
n質点系の場合は、n個の節があり、n個の固有周期があるということです。また、n次振動モードによるn次固有周期まである、ということになります。そして、どの質点系モデルにおいても一次振動モードによる1次固有周期が一番長くなリます。
3質点系モデルでも1次振動モードがゆったり動きそうなのに対して、3次質点系モデルはガクガクと振動が小さくなりそうですね。
問題としては以下のように出題されます。
過去問題より
(R06-07より)
2 . 1 次の振動モードに対応する周期は、一般に、 2 次の振動モードに対応する周期より長い。
こちらはの枝は正しいでしょうか、それとも誤り?
減衰定数
「減衰」とは…
振動が時間の経過とともに小さくなる現象、のことです。
「減衰定数」とは、その度合を示したものになります。
一般的に、減衰定数が小さいものほど、大きい振幅の振動を発生させることになります。
過去問題より
(R03-07)
4.鉄筋コンクリート造建築物の内部粘性減衰の減衰定数は、一般に、鉄骨造の建築物に比べて大きい。
こちらはの枝は正しいでしょうか、それとも誤り?
地震応答スペクトル
「地震応答スペクトル」とは、地震波の表示方法の一つのことです。
ここで問われるのは周期が長くなった場合に、地震動の応答スペクトルはどうなるのか、です。
図で見るとわかりやすいです。こちら↓(いびつな図ですいません。)
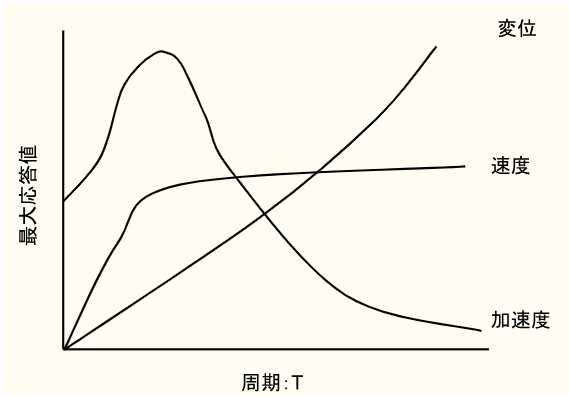
つまり、周期が長い場合…
応答変位は、大きくなる。
応答速度は、変化しない。
応答加速度は、小さくなる。
ということになります。ちなみに、減衰が大きくなると、いずれの値も小さくなります。
過去問題より
(R03-07より)
1.地震動の変位応答スペクトルは、一般に、周期が長くなるほど小さくなる。
こちらはの枝は正しいでしょうか、それとも誤り?
まとめ
いかがでしたでしょうか。
固有周期の範囲は、質点系モデルの問題がキャッチーなので印象に残りやすいですが、文章問題も出題されます。特に近年はその傾向が強くなったのでは、と思います。文章問題の場合は、今回まとめたようなちょっと知っていないと解答できない問題になっていますので注意が必要です。
今回は以上になります。少しでも皆様のお役に立っていれば嬉しいです。




コメント