音源には点音源、線音源、面音源など様々なパターンがあり距離が音源からの観測点のまでの距離が変わると、それぞれ異なった音の強さに変化します。過去問をそのまま字面で覚えようとすると、試験の当日までに忘れてしまうかもしれません。これについてはモデルがありますので、そこから仕組みを理解すれば忘れた頃に出題されても対応できます!

騒音を小さくするためには、どの程度離れる必要があるかなどの考え方と同じです。例えば、高速道路上の騒音は線音源で検討します。
「音の強さ」と「音の強さのレベル」
そもそも「音の強さ」と「音の強さのレベル」は別物なので一緒にしないようにしましょう。
それぞれの表し方
「音の強さ」とは
I(単位:W/m²)
単位面積を単位時間に通過する音のエネルギー。
「音の強さのレベル」とは
IL(単位:dB) = 10log(I / I₀)
I :観測音(W/m²)、I₀: 基準音の強さ(W/m²)
音の物理量をウェーバー・フェヒナーの法則に当てはめ、人間の感覚に換算したもの
ここでは、「音の強さのレベル」が対数を用いた表示であり、「音の強さ」とは別なもので、単純に強さを2倍にしたからといって、レベルが2倍になるということがない、ということが分かれば大丈夫です。
それぞれの関係について
それぞれの関係については、計算で求められますが、ここでは以下の2式のみ丸暗記してしまいましょう。
音の強さ(x2) = 音の強さのレベル(+3dB)
→音の強さが2倍になると、音の強さのレベルは3dB大きくなる。
ちなみに計算だと、10log(2I/I₀)=10log(I/I₀)+10log2=10log(I/I₀)+10×0.301=10log(I/I₀)+3(dB)となる。
音の強さ(x10) = 音の強さのレベル(+10dB)
→音の強さが10倍になると、音の強さのレベルは10dB大きくなる。
10log(10I/I₀)=10log(I/I₀)+10log10=10log(I/I₀)+10×1=10log(I/I₀)+10(dB)となる。
これが覚えられると、音の強さ4倍や100倍を導くことができる。
音の強さが4倍になると…
音の強さ(x4) = 音の強さ(x2x2)
= 音の強さのレベル(+3dB+3dB)= 音の強さのレベル(+6dB)
音の強さが100倍になると…
音の強さ(x100) = 音の強さ(x10x10)
= 音の強さのレベル(+10dB+10dB)= 音の強さのレベル(+20dB)
ちなみに音の強さが1/100になると、符号が逆になるだけなので、−20dBとなる。
よく出題される数値は下の表にまとめました。
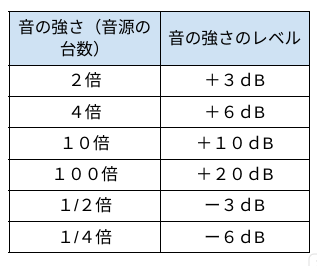
音の合成
参考までに補足しますと…
同じエネルギーの音が2つ合成されると、以下のようになります。
・音の強さ → 2倍
・音圧 → √2倍
伝搬距離と音の強さのレベル
ここからが本題ですが、非常に簡単です。それぞれの音源の性質ごとモデルを用いて確認してみましょう。
点音源
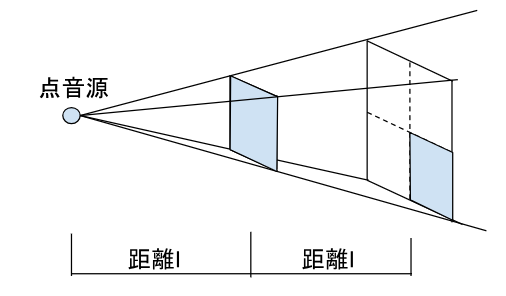
距離が2倍になることで、面積が4倍になっています。面積が4倍になることで音の強さは1/4倍になりますから、音の強さレベルはー6dBになります。
点音源は、特定の一箇所からの騒音で、距離の2乗に反比例して音の強さが減少します。
線音源
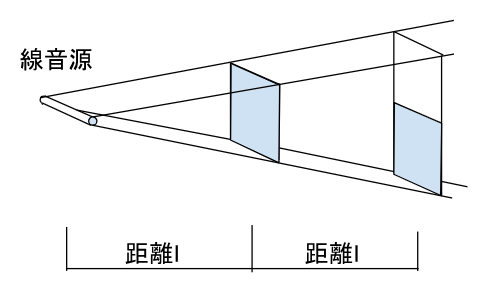
距離が2倍になることで、面積が2倍になっています。面積が2倍になることで音の強さは1/2倍になりますから、音の強さのレベルは−3dBとなります。
高速道路上の密な走行の騒音のモデルとして用いられます。線音源は、距離に反比例して音の強さが減少します。
モデルからもわかるように線音源のほうが点音源より距離による減衰が少なく、騒音で考えた場合により遠方まで影響が出ると考えることができます。
面音源
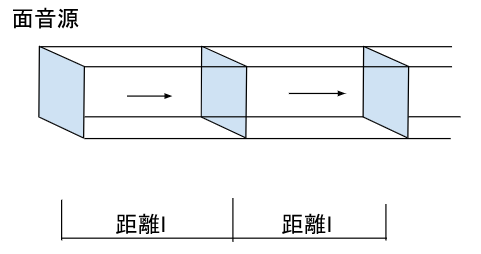
距離が2倍になっても、面積の大きさは変わらず、音の強さに変化は生じません。
面音源は無限に広い面からの騒音を想定し、タワーマンションの下層からの騒音の検討にこのモデルが用いられます。
面音源の場合は、距離による減衰はほとんど見込めません。
仕組みがわかってしまえば、数値が思い出せなくてもモデルのイメージから解答を導くことはできるかと思います。以上になります。少しでもお役に立てばうれしいです。




コメント